Applications of Mathematics in Computer Science (MACS)

Algorithmic Differentiation

Concepts:

  • gradient-based optimization;
  • symbolic differentiation;
  • numerical differentiation.

David Tolpin, david.tolpin@gmail.com

Optimization

$$z = −(x^2 + y^2) + 4$$
$$\arg\max\limits_{(x, y)} z = (0, 0)$$

Optimization

  • Given: a function $f : A \rightarrow \mathbb{R}$
  • Find: $x_0 \in A$ such that $f(x_0) \le f(x)$ for all $x \in A$ — "minimization", or $\ge$ — maximization.

Examples

  • shortest path in graph
  • job with highest salary
  • best vaccination strategy for COVID

Stochastic optimization

We can try many values randomly:

Gradient-based optimization

Gradient: $\nabla f = \begin{pmatrix} \frac {\partial f} {\partial x_1}\\ \frac {\partial f} {\partial x_2} \\ ... \end{pmatrix} $ — direction of fastest ascent.

With $\nabla f(x, y, ...)$ we can optimize much faster.

Gradient descent

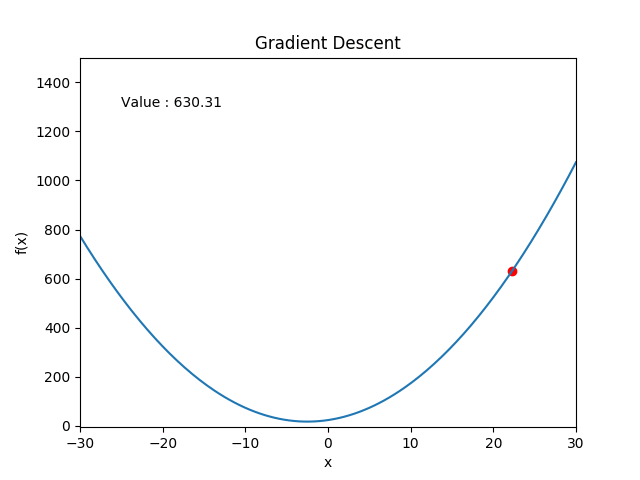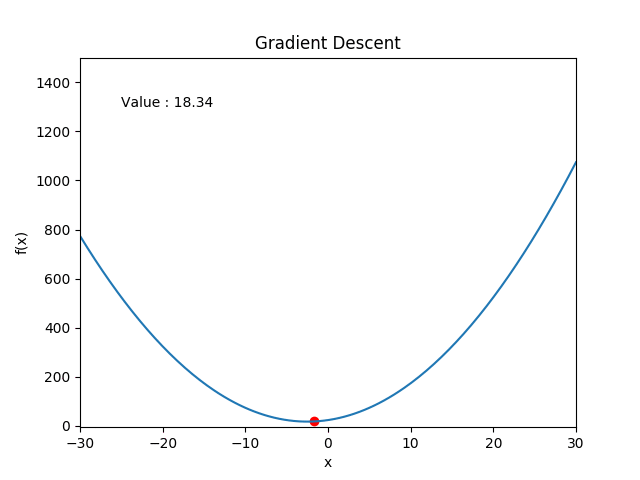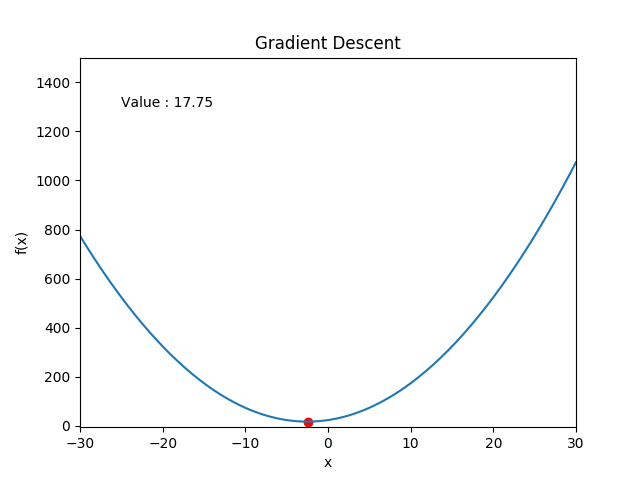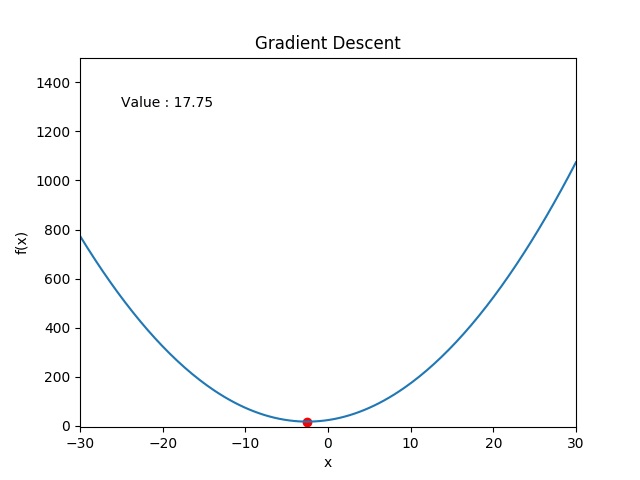
  • Repeat:
    1. $x \gets x - \delta\nabla f(x)$
    2. $\delta \gets \gamma\delta$
  • where
    • $\delta$ is small
    • $\gamma = 1 - \varepsilon$

Newton's method

  • Repeat:
    1. $x \gets x - \frac {f''(x)} {f'(x)}$
  • converges faster than GD

How to obtain derivatives?

$$\nabla f(x)$$ $$f'(x)$$ $$f''(x)$$ $$...$$

Differentiation

  • Slope of the function's tangent
  • $f'(x) = \lim\limits_{h \to 0} \frac {f(x+h) - f(x)} {h}$
  • also $\frac {df} {dx}$ (Leibniz's notation)
  • Partial derivatives: $\frac {\partial f(x_1, x_2, ..., x_n)} {\partial x_i}$

Differentiation rules

  • Constant rule: if $f(x)=C$ then $f'(x)=0$
  • Sum rule: $(f(x) + g(x))' = f'(x) + g'(x)$
  • Product rule: $(f(x)g(x))' = f'(x)g(x) + f(x)g'(x)$
  • Quotient rule: $\left(\frac 1 {f(x)}\right)'=-\frac {f(x)'} {f(x)^2}$
  • Chain rule: $f(g(x))' = f'(g(x))g'(x)$

Differentiation examples

$$1' = 0$$ $$x' = 1$$ $$\left(x^2\right)'= xx' + x'x = 2x$$ $$sin(x)' = cos(x)$$ $$tan(x)' = \left( \frac {sin(x)} {cos(x)}\right)' = \frac {sin^2(x) + cos^2(x)} {cos^2(x)} = \frac 1 {cos^2(x)}$$ $$...$$

How do computers differentiate?

  • Numerical differentiation
  • Symbolic differentiation
  • Algorithmic differentiation

Numerical differentiation

  1. Choose $h$
  2. Compute $f(x)$
  3. Compute $f(x+h)$
  4. Return $\frac {f(x+h) - f(x)} h$

Problems

  1. $h$ too large — truncation error (שגיאת קיטום)
  2. $h$ too small — roundoff error (שגיאת עיגול)

Symbolic differentiation

  1. Represent function symbolically.
  2. Apply differential rules.

Problems

  1. Loops, conditionals, recursion.
  2. Code swell:
    \begin{equation} \begin{aligned} \left( \frac {\log(x) + \exp(x)} {\log(x)\exp(x)}\right)' = & -\frac {\exp(-x)(\log(x)+\exp(x))} {\log(x)} \\ & -\frac {\exp(-x)(\log(x)+\exp(x))} {x\log^2(x)} \\ & + \frac {\exp(-x)\left(\exp(x) + \frac 1 x\right)} {\log(x)} \end{aligned} \end{equation}

Algorithmic differentiation

  • NOT symbolic differentiation
  • NOT numerical differentiation
  • differentiates ANY code
  • computation costs of $f'(x)$ and $f(x)$ are similar

Algorithmic differentiation


                        def f(a, b):
                          c = a*b
                          d = sin(c)
                          return d
                        

                        def f(a, da, b, db):
                          c, dc = a*b, da*b + a*db
                          d, dd = sin(c), dc * cos(c)
                          return d, dd

Program trace

f.py


                        def f(a, b):
                          c = a*b
                          if c > 0:
                            d = log(c)
                          else:
                            d = sin(c)
                          return d

f(2, 3)


                        a=2, b=3
                        c=a*b=6

                        d=log(c)=1.791


                        return d=1.791

f(2, 3), df(2, 3)/da


                        a=2, b=3, da=1, db=0
                        c=a*b=6,  dc=da*b + a*db=3

                        d=log(c)=1.791, dd=dc*(1/c)=0.5


                        return d=1.791, dd=0.5

Application examples

Open In Colab